Some Remarks on the Nature of Trochees and Iambs and their Relationship to Other Metres

Some Remarks on the Nature of Trochees and Iambs

and their Relationship to Other Metres

The iambic is the characteristic rhythm of people as they talk […]. The trochaic rhythm, again, is too much akin to the comic dance, as may be seen in tetrameter verse, for the rhythm of tetrameters is light and tripping. (Aristotle, 1932: 3.8, 1408b).

His rage armed Archilochus with his iambic: comedy and tragedy have adopted it, as being natural for dialogue, able to drown out the noise of the audience and suited to action (Horace: 1951, 117).

This paper was written back in 1971 and published as Chapter 3 of my Perception-Oriented Theory of Metre,. Recently I realized that metrists are still puzzled as to the difference between the iambic and the trochaic, and the special status of the iambic, already pointed out by Aristotle and Horace. Since my book A Perception-Oriented Theory of Metreis inaccessible today, I decided to republish this paper as it appeared in that book, with some updating and minor corrections.[1]

The present study assumes, following Wellek and Warren, that poetic rhythm in the tonic-syllabic system current in English poetry can be best accounted for by three sets of patterns: First, an abstract matrix of expectations consisting of regularly alternating strong and weak positions. Secondly, the stress-pattern of spoken language.  Some aspects of this stress pattern confirm the abstract schema (one could even say that it is from these that the reader abstracts the metric pattern); some aspects deviate from it, and produce tension. These deviations, far from being signs of imperfection, of “unmetricality”, are major prosodic and expressive assets. When the reader encounters some deviation from the abstract metric pattern, he makes adjustments in its performance, so as to preserve both his metrical set, that is, his feeling of regularly alternating strong and weak positions and, at the same time, the stress pattern of his spoken language. The adjustment frequently consists in overarticulation, overstressing, and additional grouping of stresses. This constitutes the third pattern, the pattern of performance. The greater the deviation, the greater the adjustment required and the tighter the additional grouping, One of the basic assumptions of the present study is, then, that the rhythm of a poem is accessible only through some kind of performance; an adequate account of a poem’s rhythm can be given only by considering the interplay of three patterns: those of metre, stresses and performance.

A lexically stressed syllable confirms metre in an s position, an unstressed one—in a w position. Consider, for instance, Donne’s line:

(1)

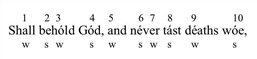
The expected pattern of alternating w and s positions is confirmed in positions 1, 4, 5, 6, 7, 8, 10. In positions 2, 3 and 9 it is infirmed. Overarticu­lation, overstressing and additional grouping of the performer, however, may render the line acceptable to the ear as iambic metre. By grouping together syllables 8, 9 and 10, we get a sequence of three stresses, two of which coincide with s positions. In this group, “deaths” can be pronounced as stressed, though relatively less heavily than the adjacent syllables, preserving the basic iambic cadence of the line.  The deviant stress can be tolerated only so far as the metric pattern is emphatically reinstated in the two strong positions of the group.  Alternatively, one may perform the sequence as a group ofequally stressed syllables. In this case, the reader’s “metrical set” has to rely on the mind’s inclination to memorize and anticipate the repetition of an initial pattern, creating counterpoint (and tension) between the two sets. Overarticulation of the three stressed syllables is needed to make mental processing space available for the parallel processing of conflicting stress and metre. Thus, overarticulation and additional grouping are a means of avoiding chaos while preserving the stress pattern of ordinary speech.

In positions 2 and 3, it is more difficult to preserve the stress pattern and avoid chaos. Evidently, –hold cannot be performed so that both adjacent syllables are more heavily stressed while preserving, at the same time, the stress pat­tern of ordinary speech, The most obvious performance here would be to overstress and overarticulate  –hold, and to group together tightly the first four syllables, which would yield a symmetrical, fairly “simple” gestalt: two unstressed syllables balanced against two stressed ones­. There is an impetuous drive to reach the fourth position, where the stress pat­tern and metric pattern have “coinciding downbeats”.  Here, the metric pattern is “reconditioned” and becomes “fresh and new”—to use Leonard B. Meyer’s phrases (1956: 118), I would suggest that the counterpoint in positions 1–4 builds up greater tension than in positions 8-10 and, altogether, they produce an uncommonly deviant (and tense) line which can still be perceived as rhythmical.

The Trochaic

The peculiar nature of the trochaic metre has frequently drawn attention. Time and again, critics feel a necessity to account for this peculiarity. In the follow­ing, I shall add yet another item to the list of would-be explanations and hope to demonstrate its explanatory force. “It is interesting to note”, writes Chatman, “that lighter syllables seem more readily ictic in trochaic than in iambic feet” (1966: 140–141). “The trochaic mode more easily violates normal prose accentual patterns; it quite insists on dominating the rhythm. Iambic verse seems not to exert its will so rigidly” (p. 141). As an explanation for this peculiar character, Chatman quotes Halpern, and then offers to substitute his own explanation:

Halpern’s thesis is that trochaic verse, along with anapestic and dactylic, is a subspecies of the native Germanic strong-stress verse, which he feels is both isoaccentual and isochronic [...] I think his observations about the relative inflexibility of the trochaic verse are correct, but would suggest another cause, namely the comparatively short history of the mode. The sophisticated smoothness of the iambic verse has been long in developing; trochaic verse, however, was not taken very seriously in England until the nineteenth century (141, n.)

Both explanations have the same weakness: neither the Germanic strong-stress verse, nor the history of the English metre are perceptual features of an actual piece of trochaic poetry. As Coleridge put it, “nothing can permanently please which does not contain in itself the reason why it is so, and not otherwise” (Biographia Litera­ria,Chapter 14).A child who attends to “Tackle, tackle, Mother Goose,/ Have you any feather loose?” responds to the peculiar trochaic quality in the poem with no particular instruction in the history of English and Germanic verse. Furthermore, nursery jingles in Hebrew are preferably written in the trochaic metre. Russian poets and critics feel that the trochaic metre has a particularly “encouraging, optimistic, vigorous” quality. I take this to be a manifestation of the “dominating” character of the trochaic, its tendency to “exert its will”. At any rate, a satisfactory explanation of this peculiar trochaic quality will also have to account for the greater rigidity of ternary metres and the greater flexibility of the iambic.

Jespersen, too, has pointed out an asymmetry between trochaic and iambic lines. Whereas one may “invert” the first foot of the latter, “substituting” a trochaic for an iambic foot, the former seems not to tolerate the “substitution” of an iambic for a trochaic one (reported by Halle and Keyser, 1966: 199; cf, Beaver, 1968: 314). Halle and Keyser’s theory of “stress maxima” offers an ex­planation of why the first foot of an iambic line suffers “inversion” more than the subsequent feet. They, however, try to apply this theory to the alleged in­tolerance of inversion in the trochaic line too. Their argument is supplemented by Beaver. The first and last syllables of a line (or of a syntactic unit) cannot be a stress maximum: they have no “two adjacent syllables” to bear less “linguistically determined stress”. In such iambic lines as Shakespeare’s “Proving his beauty by succession thine” (Beaver, 1968: 318) and Keats’ “Silent upon a peak in Darien” (Halle & Keyser, 1966: 189), the “inversion” is usually accepted as perfectly regular because, they say, it results in no stress maximum in a weak (odd-­numbered) position

As for the trochaic, Halle & Keyser observe that Longfellow’s “‘Life is but an empty dream’ is rendered unmetrical if the initial trochee replaced by an iamb as in [...] ‘To live’s but an empty dream’. The reason for this asymmetry between iambic and trochaic lines is clear once it is realized that trochaic verses have stress maxima only at odd positions in the verse and that an initial iambic foot locates a stress maximum on the second (i,e., on the even) position in the line, in direct violation of the trochaic principle” (p. 199).

This explanation, at last, refers to perceptual features of actual verses. Beaver adds his own example. He changes Longfellow’s trochaic line “Straight between them ran the pathway”, to read “Between them straight ran the pathway”, “We have created”, he says, “a stress maximum in an even position, thus violating the rule of trochaic meter” (p. 319). This, then, seems to account for the asymmetry of the two metres. Unfortunately, however, the examples are asymmetrical in their own right, so that if there be any asymmetry of the metres, the explanation should be sought for elsewhere.

The first foot of an iambic line can be “inverted” if the iambic pattern is reasserted, or at least not violated, in the second foot. If the second foot is “inverted” too, it creates a stress maximum in the third (weak) position, as in the construct

            (2)       

There is no asymmetry in this respect between iambs and trochees. By the way, such instances do occur in English poetry, but are explained away by Halle and Keyser as “the Italian influence of double trochee” which, again, “does not contain in itself the reason why it is so, and not otherwise”.

What happened, then, to the Longfellow examples and their transcriptions? One should notice that in Longfellow’s trochaic lines the reader has a feeling of artificiality.  Consider the following two lines:

(3)           Straight between them ran the pathway,

                Never grew the grass upon it...

(Beaver’s italics, to mark what he regards as stress maxima). This kind of artificiality is absent from Blake’s “The Tyger”, for instance: “What the anvil, what the chain”, or any other line. I shall point out only one of the many sources of difference. In actual speech (and according to the definition fostered by Halle, Keyser and Beaver), conjunctions and prepositions have no syllables that bear lexical stress. In the Longfellow lines, two strong positions are occupied by prepositions ( and ). Because of the compelling nature of the trochaic metre (whatever its cause), Beaver marked them as stress maxima (contrary to his definition) and this is, indeed, the way we are disposed to recite these verses, al­though this is not linguistically justified (the stresses are “allophonic”). In Blake’s poem, Beaver could not assign a single stress maximum to any preposition or conjunction.

In the line “Life is but an empty dream” (metrically identical with Blake’s line) the second strong position is occupied by “but”. Between two syllables with reduced vowels, a copula (is) and an article (an), it appears as a stressed syllable. In the “inverted” version “To live’s but an empty dream”, after a stressed syllable and a jam of three consonants (vsb) “but” is perceived as less prominent. Thus, in a “trochaic” line of seven syllables, only one unambiguous realization of trochaic foot is left (). On the other hand, if we decide to assign stress on the adverb “but”, and duly emphasize it in performance (), we receive in positions two and three, back to back, two stressed syllables and the line becomes similar to some perfectly legitimate trochaic lines, as we shall see. At any rate, the line will be “metrical” under the stress maxima theory itself. The question is, then, not whether a trochaic line can bear “inversion” of its first foot, but rather whether “but” can bear full lexical stress. This example, then, does not prove that trochaic lines do not tolerate “inversion” of their first foot.

Beaver’s transcription is not much happier. “Between them” yields not exactly a stress maximum, as Professor Beaver would like to indicate, nor does “them straight” realize exactly a trochaic foot (if anything, it has an iambic rise)

As a matter of fact, the first foot of a trochaic line can be “inverted”.  To be sure, it is not as frequent and as easy as in an iambic line. It demands the overarticulation and overstressing of the deviant stressed syllable, and very em­phatic grouping of the first two feet in order to make it acceptable. But the decisive condition is, as in the iambic line, that the metric pattern should not be violated in the second foot.  If the first foot of a trochaic line is “inverted” and in the second the trochaic is genuinely confirmed, there are, back to back, two stressed syllables and no question of a stress maximum in the second position may arise. Consider the following three examples from two poems notorious for their regular rhythms:

 (4)    a,    

          b.

          c.      

In these three examples the reader is induced to group the first three syllables tightly together. On the third position, the stresses of the trochaic pattern and the linguistic stress pattern emphatically coincide. Thus, the vigorous, dominant character of the trochee is not the result of its resistance to the “inversion” of its first foot, but rather its cause.

Similarly, Halle and Keyser are victims of their own mistaken assumption when they offer the phrase “On first looking into Chapman’s Homer” as an example of unmetrical utterance. Suppose we encounter it in an emphatically trochaic context:

(5)       

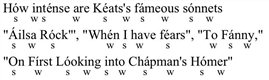
According to their definition a trochaic line would be one in which there are no stress maxima in even positions This is precisely the case here. According to the assumptions of the present study, the recognition of a line’s “metricality” presupposes a correct hypothesis, and/or proper performance.

Professor Beaver offers an alternative explanation for the peculiar character of trochaic metre:

Since most trochaic verse in English is in short lines, and since our impressions of iambic verse are derived almost entirely from pentameter, it would seem entirely possible that the issue has been falsely formulated—that the differences of rhythm encountered are attributed not to the type of foot but to the length of line in which the foot characteristically appears. And it will be argued below that the more regular beat of short-lined verse is accounted for by the fact that a much higher percentage of positions available for stress maxima are occupied than is the case in decasyllabic verse (p. 314)

One suddenly realizes that it is quite difficult to find poems written in deca­syllabic trochaic lines. Nevertheless, there are some. What is more, Halpern, as quoted by Chatman, illustrates his observation quoted above by a decasyllabic line: “... and even where reversals are indicated the reader has strong desires to ‘wrench’ the stress or accent, as in Browning’s:

What  there’s  nothing  in  the/m¬¬oon  note-/w¬orthy?”

                                                                        (Chatman, 1965: 141)

Obviously, whatever the source of this impression in this particular  instance, it cannot be accounted for by the  peculiarities of shorter-than-decasyllabic  lines. Further, although I am not quite happy with the way Professor Beaver subsequently documents his account of the rhythmic quality of short-lined verse, I am inclined to acknowledge the rhythm he attributes to it (but I prefer Aristotle’s view that the two rhythms are akin rather than that the trochee’s effect is, in fact, to be attributed to the tetrameter’s—see motto above). As for the occupancy of  “a much higher percentage of positions available for stress maxima than is the case in decasyllabic verse”, it seems to be a result rather than a cause. For simple arithmetic reasons, the shorter the line, the less it tolerates deviating feet. Where­as two deviating feet constitute more than 66.6%of a trimeter line and 50% of a tetrameter line, they constitute only 40% of a pentameter line. This, however, only means that here, too, as in the trochaic meter, poets can afford less deviations in absolute numbers if they want to preserve an impression of rhythmicality. The cooperative reader “has a strong desire to ‘wrench’ the stress or accent”, whenever needed and possible. If this indicates anything, it indicates that trochaic metre and short-lined verse have, on independent grounds, something in common: a compelling quality. This may explain why the trochaic is so scarce in deca­syllabic lines and “prefers” to dwell in shortened verse.

An alternative explanation would be that this compelling nature of the tetrameter is due to its gestalt qualities. A ten-syllable-long line cannot be divided into two symmetrical halves of equal length and equal structure. If you divide it into 5+5, in the iambic meter the first segment will begin and end with a weak position, the second segment with a strong position. In the trochaic meter the inverse will be the case. In the eight-syllable-long line, the caesura will divide it into segments of equal length (4+4), and equal structure: in the iambic metre both segments begin with a weak position and end with a strong position; in the trochaic, vice versa. Thus, the tetrameter has a stronger, more rigidly symmetrical shape than the pentameter, that is, of a more compelling nature, which more forcefully determines the character of its parts.

Trochaic metre and short-lined verse reinforce this compelling quality in each other. But we still have no explanation why the trochaic should be more compelling than the iambic. Curiously enough, the clue to it is quoted in Chatman’s book too (1965: 26-27), but he does not connect it with this specific problem.

One would imagine that in an endless series of equidistant tick-tacks no preference would be given to iambic or trochaics rhythms; the only distinction should be whether the series began with an upbeat or a downbeat. Experimental psycholo­gy, however, shows that this is not so. H. Woodrow found in his tick-tack experiments that in a series of tick-tacks, “with equal temporal spacing, a regularly recurring, relatively greater intensity exerts a group-beginning effect, and a regularly recurring, relatively greater duration a group-ending effect” (Woodrow, 1951: 1233). “Intensity has a group-beginning effect: duration, a group-ending effect: pitch, neither a group-ending nor a group-beginning effect” (Woodrow, 1911: 77).

Both Chatman and Meyer (1956) invoke Woodrow’s experiments; the latter also indicates at some length their implications for a variety of  metric feet:

When time intervals are equal, and every second sound is accented, the rhythm will appear to be trochaic. If intervals are equal and every third sound is accented, the rhythm will appear as a dactyl. Thus the trochee and dactyl may be grouped together in the sense that both are primarily products of intensity differences rather than durational differences.

Just the opposite is the case with iambic and anapestic rhythms. They are basically products of durational differences. If we start with a trochaic rhythm and gradually increase the interval after the louder sound, we arrive at an iambic rhythm. Similarly, if we begin with a dactylic rhythm and gradually lengthen the interval after the louder sound, the rhythm tends to become an anapest Thus, the greater the relative duration of one tone or beat of a group, the greater the tendency for it to complete the group, while the greater the relative intensity of a beat, the greater the tendency for it to begin the rhythmic group. In other words, durational differences tend to result in ‘end-accented rhythms’, and intensity differences tend to result in ‘beginning-accented rhythms’.

Woodrow also found that pitch has neither group-beginning nor group­-ending effect. (1956: 106-107)

As indicated above, my paper was written in 1971. Since the nineteen-eighties and nineteen-nineties, Woodrow’s work in non-linguistic tick-tacks has had an enormous impact on linguistic research, in a very different perspective. To mention only a few studies: The generative linguist Bruce Hayes applied Woodrow’s extra-linguistic principle of rhythmic grouping to iambic and trochaic feet in a wider linguistic perspective:

a. Elements contrasting in intensity naturally form groupings with initial prominence.

b. Elements contrasting in duration naturally form groupings with final prominence.

He was more interested in generalizing to a cross-linguistic theory of stress assignment than in versification, and his work is motivated by in-depth analyses of stress patterns of a large number of languages (for a critique of Hayes, see Anthi Revithiadou,2004).

In Chapter 5 of his doctoral dissertation, Curt Rice (1992) replicated Woodrow’s experiments. “The technological resources for conducting this research are dramatically more sophisticated than those which Woodrow had available”. At variance with Woodrow, Rice (1992:198) showed that variations in pitch do lead to a significant shift towards iambic groupings, a result that, Revithiadou (2004: 38) says, does not lend support to Hayes’s Iambic/Trochaic Law. But it lends additional support to the view expressed here. The reason for this difference appears to be that we have different purposes: Hayes applies the extralinguistic principles of rhythmic grouping to phonological stress rules, while I apply them to versification patterns determined independently from linguistic patterns, as suggested by Halle and Keyser.

Now, coming back to verbal rhythms, spoken language consists of syllables of varying duration. Schramm (1935), Fry (1958), and Chatman (1965) have demonstrated that the acoustic cue to stress is a complex of pitch, duration, loudness, in this order of decreasing effectiveness. Usually, at least two of these three components are present. If pitch differences are irrelevant to grouping direction and duration differences are more effective in stress perception than amplitude differences, end-accented metres should be more natural in poetry in a variety of languages. If variations in pitch also lead to a significant shift towards iambic groupings, it should reinforce this effect. Significantly, even in Hungarian poetry, where stress is invariably on the first syllable, the iambic metre is far more natural and widespread than the trochaic.

In “stress-timed” languages pitch-obtrusion seems to be predominant; it is usually reinforced by duration or loudness or both. Thus, in an “end-accented” metre like the iambic, there is room for complex interplay between pitch, loudness and duration. In the trochaic, on the contrary, the inherent properties of “beginning-accented” metres demand the suppression of duration differences, and the bestowal of priority upon loudness (reinforced by pitch) in effecting stress. Characteristically enough, Chatman remarks: “Brown also dis­covered an interesting difference between iambic and trochaic nonsense lines; ictus in iambic meter was from 2.1 to 2.9 times longer than non-ictus, whereas in trochaic meter, the ratio was profoundly different, the ictus ranging only .46 to 1.04 times the length of the non ictus” (p. 79).

Thus, when performing a trochaic poem, the reader tends to suppress quantity, which in English is merely an optional diversifying element. In this manner, the contrast between stress and no stress is cued by amplitude differences, and the contrast between longer and shorter syllables suppressed as much as possible. If the verbal material permits, the trochaic will sound simple, single-minded, straightforward, vigorous, optimistic, encouraging and the like. Consider:

(6)           When the wind is in the east,

                Then the fishes do bite least;

When the wind is in the west,

Then the fishes bite the best.

“Bite” in line 4 falls in a strong (odd) position and it is duly stressed. In line 2 it falls in a weak (even) position and should create metric complexity But the reader prefers to suppress it and rather stress the preceding auxiliary verb (do), which is unemphatic here, introduced mainly for the metre’s sake. Such a tendency for regularity may be reinforced by the repetition of some notoriously trochaic word or sound pattern in the first line, e.g. “Handy spandy Jack-a-Dandy”, “Tackle, tackle, Mother Goose”, or “Tyger, tyger, burning bright”. Such a sound pattern will tend to perpetuate its trochaic cadence in the subsequent lines A glance at Carey’s parody on Philip’s too smooth style may be revealing:

(7)           Nauty Pauty Jack-a-Dandy

                Stole a piece of Sugar-Candy

                From the Grocer’s Shoppy-shop,

                And away did Hoppy-hop.

Compare to this the genuine, less smooth nursery rhyme:

(8)           Handy spandy, Jack-a-Dandy,

Loves plum cake and sugar candy;

He bought some at the grocer’s shop,

And out he came, hop, hop, hop, hop.

After having established in the first line a conspicuous trochaic lilt, we feel that trochaic rhythm is more disturbed by “plum” in a weak position, than by the “extrametrical” syllables (he, and) at the beginning of lines 3 and 4. “Plum” is not only a stressed syllable (“neutralizing” the contrast between stressed and un­stressed syllables).  It also seems to be too long for squeezing between two down­beats. It upsets the time-scheme of the performance (it should be remembered that timing is a part of performance pattern and not of the poem itself). On the other hand, the poem would not bear a “weighty” performance which could anticipate a stressed long syllable in a weak position. The word begins with a “jam” of four consonants (vspl) and ends with a jam of two (mc). Similarly, the alternating hops “insist” on their equal length and stress with the adjacent hops, and so “resist” being turned into upbeats The parody avoids such “inconveniences” seeing to it that all the unstressed syllables allow isochronic and isoaccentual performance, with no undue slowing down of tempo. Consider one more point regarding the extrametric words at the beginning of lines 3 and 4 (He and And). They ought to turn, instantly, the trochaic verse into iambic; but if you suppress duration differences as much as possible, the trochaic character will be largely preserved.

That is also why Professors Halle, Keyser and Beaver may feel that the first foot of a trochaic line cannot be “inverted” like that of an iambic line. The trochaic metre resists complexity, the reader “has a strong desire to ‘wrench’ the stress or accent” when the foot is “inverted”. Performance cannot “compensate” by bringing in, for example, an interplay between the intensity factor and the time factor. When, finally, the first foot of a trochaic line is “inverted”, it demands stronger overstressing, overarticulation and additional grouping than an iambic line, as well as suppression of duration differences. If this occurs in an in­tense and complex poem, as is the case with

(9)             

the reader feels that the rhythmic complexity is sufficiently motivated.

Or, consider the first four lines of Browning’s “Soliloquy of the Spanish Cloister.” They arouse ingeniously two incompatible, equally strong desires: “to wrench” the prose stress pattern in favour of the trochee and, at the same time, to preserve it.

(10) 

The pace for both desires is set in the first line. The metre of this line is as regular as one could expect in a trochaic (with, probably, the need to suppress a possible stress on ‘there’, used interjectionally). The metric pattern is reinforced by the stress pattern coinciding with it which, in turn, is reinforced by a recurring sound pattern, not the simple kind such as “Tackle, tackle” or “Tyger, tyger”, but rather a very sophisticated version of the type “burning bright”, The contrast between s and w position is heightened by a sophisticated string of alliterations, emphasizing the s positions, culminating in horr-. It repeats the rs of the first, the o of the second, and the h of the third s position. Go (preceded by an r) repeats the sounds of G-R-R-R. An important keyword is Gr-r-r. As a nonsense word, it fulfills the function of nonsense words at the beginning of nursery rhymes: to draw attention to the sound pattern. As an emotive or onomatopoeic word, it arouses a strong desire to preserve the rhythms of colloquial language. The first word of the second line (“Water”), confirms the trochaic pattern. The next stress, however, is displaced to a w position. The strong desire “to wrench” the prose stress here is vigorously counteracted by the colloquial character of “damned”. The only option left for the reader is to accommodate both patterns in an exceptionally tight additional grouping, while both seek to establish themselves as strongly as possible in his perception.[2] After all this, the reader is ready for any grouping and overarticulation required to per­form the deviating feet . The rest of the line reasserts the trochaic. If emphatic stress is assigned to the pronouns “mine”, “you”, the fourth line becomes “metrical”, it may even corroborate one’s metrical set, despite the six heavily stressed syllables in a line of seven (How acceptable this is here, as contrasted with “Loves plum cake” in the nursery rhyme!).

A word may be said about the metre of Shelley’s “To a Skylark”. This poem has, for some reason, puzzled some of our leading prosodists. The problem is whether its metre is iambic or trochaic. To tell the truth, this question appears to me similar to the question “is the zebra white with black stripes, or black with white stripes?” Or, to put it more mildly, ‘is “The Rhyme of the Ancient Mariner” tetrametric or trimetric verse?’ Unless our purpose is book-keeping or classification, none of these questions should trouble us. The problem arises not only because the fifth line of each stanza is iambic whereas the preceding ones are trochaic, but also the second and fourth lines of each stanza begin and end in a strong position. Therefore, they are said to be “ambiguous”: one cannot know whether they are iambic with the first position unoccupied, or trochaic with the last position unoccupied. In light of Woodrow’s experiments with extralinguistic tick-tacks and Brown’s experiments with nonsense lines, if you suppress duration differences the lines will be perceived as trochaic, if you carefully preserve them, they will be perceived as iambic. In view of the Gestalt rule of Good Continuation, there are good reasons to suppose that performers will tend to preserve the trochaic character of the first four lines of each stanza. So, we must decide what is more important: the name of the metric structure, or its perceived character.

Professor Beaver writes: “As a matter of fact, many poets have capitalized on this ambiguity. In ‘To a Skylark’, Shelley chooses a stanza form which maintains the ambiguity through the first four lines of each stanza, resolving it in the iambic hexameter fifth line” (1968: 317). Let us have a look at the first stanza of the poem:

(11)         Hail to thee, blithe Spirit!

       Bird thou never wert,

That from Heaven, or near it,

       Pourest thy full heart

In profuse strains of unpremeditated art.

In fact, only two of the lines (2, 4) can be said to be ‘ambiguous’. Lines 1 and 3 are unambiguously trochaic, and line 5 is unambiguously iambic.  Putting aside the problem of the fifth line for the time being, one may observe that the reader of French, German, Russian, Hungarian and Hebrew poetry (and possibly that of many other languages) is familiar with the alternation of “feminine” and “masculine” rhymes, that varies rhythm without basically changing the metre. In English, it is more difficult to do this because of the scarcity of “feminine” rhymes.

All that happens here is, then, an extension of the grouping principle of performance when irregularities occur. The dissimilarity of the odd-numbered and even-numbered lines upsets their balance to some extent and they demand some further grouping. By grouping line 1 with 2, and line 3 with 4, the four-line unit is divided into two corresponding halves, reinforcing the grouping effect, of the rhyme-scheme. (This is, precisely, with the necessary changes, what happens in the ballad stanza too. The asymmetry of the tetrameter and the trimeter lines requires grouping them into two symmetrical groups, thus enhancing the unity and simplicity of the stanza).

I am inclined, then, to disagree with Professor Beaver’s more general “solution” to poems like Tennyson’s “Lockley Hall”. “An obvious solution to this problem is to view such poems orportions of poems as metrically ambiguous in their surface structure, and postulate that they are, in their deep structure, either iambic with initial position always unoccupied, or trochaic, with final position always unoccupied” (1968: 317). The problem will not arise at all if we realize that the obligatory caesura divides the lines of this poem, or of “A Toccata of Galuppi’s”, so that their metric structure is exactly the same as those of the Browning poem discussed above. The typographical re-arrangement of these lines only lends support to the grouping arising from the asymmetry of feminine and masculine endings:

(I 2a)  Comrades, leave me here a little, while as yet ‘tis early morn:

            Leave me here, and when you want me, sound upon the bugle-horn.

(I 2b)      Comrades, leave me here a little,

                  While as yet ‘tis early morn:

            Leave me here, and when you want me,

                 Sound upon the bugle-horn.

(13a)  Oh Galuppi, Baldassaro, this is very sad to find!
I can hardly misconceive you; it would prove me deaf and blind;
But although I take your meaning, ‘tis with such a heavy mind!

(13b)  Oh Galuppi, Baldassaro,

                 This is very sad to find!

            I can hardly misconceive you;

                 It would prove me deaf and blind . . .

The ‘unexpected’ appearance of the iambic hexameter at the end of Shelley’s stanza resolves, in fact, nothing. It rather complicates things further. It does not reveal the ‘deep structure’ of the preceding lines; it deviates from them. According to Barbara Herrnstein-Smith (1968), closural effect can be achieved by deviating from a previously established structural principle. This would imply a hierarchy of grouping principles operative in the stanza. (1) The line, (2) two pairs of lines parallel to each other, (3) a fifth line deviating inlength and foot, emphatically sealing the stanza. Whether it actually does so, depends on whether the reader realizes the hierarchy of grouping principles, or loses sight of this third, widest one.

Wimsatt and Beardsley seem to be after a far more deeply-seated quality when they remark on the first line of this poem:

The inquestionably iambic movement following the very strong first syllable might, if we were desperate, be accounted for by saying that the word “Hail” breaks into two syllables, “Hay-ul”, with a resultant needed extra syllable and the familiar opening pattern of iambic inversion. But a much more energetic and irrefutable assertion of the iamb appears to be in the progressive rise or stress increase of the three syllables “thée,      bl¡ithe, sp¡írit”. (1959 593-4)

This argument seems invalid to me.  Even if we take for granted, for the sake of the present argument, four degrees of stress “to thée, bl¡ithe, sp¡írit”, the only thing we must do in order to refute this conception of “rising” rhythm is to say that the energetic iambic rise is followed by a sudden trochaic fall and that in every trochaic line the final falling movement is preceded by a rising movement In fact, the term “iambic movement” is used here in a figurative sense: it doesn’t refer to the recurring metrical pattern of feet, but to the over-all rising pattern of performance.

In a note, they add: “But many such lines, like the one from Shelley’s ‘Sky­lark’ [... ], can be shown in one way oranother to be in fact iambic. The shape of the phrases is likely to have much to do with it”’ (p. 594).

The  line  has  been  suggested,  but  not  shown,  to  be  iambic.  Formally,  the  line is nothing but trochaic. But what is it that impresses the critics as so “untrochaic” in this line? It is its complexity. “Blithe” consists of one stressed syllable with a diphthong as its nucleus. Neither its stress nor its length can be sufficiently reduced and fitted into a weak position so as to equal to in the preceding weak position. Thee in the preceding strong position bears no lexical stress. The regular contrast of intensity, as well as the equal duration of feet, is upset; this makes the line more like iambic. The stressed syllable in a weak position can be accommodated only by additional grouping; this was, indeed, done by Wimsatt and Beardsley and this makes the line too complex for an ordinary trochee. But now that we know what is so “untrochaic” about the line, we need worry no more, and there seems to be no reason why we shouldn’t continue calling it “trochaic”.

Iambic Tension

The iambic is usually thought to be the most natural metre, the nearest to ordinary speech rhythms. A striking feature of this measure is that in languages as different from English as Hebrew and Hungarian, poets use it in a manner very similar to English blank verse. [Note 2010: this is particularly noteworthy in Hungarian, where the end-accented nature of the iamb generated by duration differences overrides the fact that in Hungarian the first syllable of a word is invariably stressed). This seems to hold true even outside the syllabotonic system, as Aristotle and Horace may bear witness, for whom Iambic meant a “quantitative” measure, alternating longer and shorter syllables (see motto above).

It is difficult to know now exactly what Horace meant by the last two phrases, but the fact that the iambic was found to be “natural for dialogue” remains. As we have seen, Aristotle agrees: “The iambic is the characteristic rhythm of people as they talk”. Our explanation of its nature will have to take this fact into account.  At the end of his “‘Prose Rhythm’ and Metre”, Roger Fowler (1966: 99) comes to the following conclusion­:

This, paradoxically, may help to explain why the iambic measure is felt to be suited to English: not because its pattern corresponds to the prose rhythms of language, for it does not; but because it necessitates a constant syncopation of prose rhythm against its own rhythm, inviting poets to be metrically complex, not to jog along with simple regularity.

Surprising as this may be, the great variety of languages to which the iambic measure seems to be “suited” (even to Hungarian!), supports this conclusion. I would, however, prefer “tolerates” to “necessitates”. Verbal necessity alone cannot account for syncopation; it cannot explain why Pope should resort to syncopation less frequently than Milton (as Fowler himself asserts), or why Shakespeare, in his earlier work, should resort to it less frequently than in his later work. It seems, rather, that syncopation is related to wider issues and that it takes deliberate daring to abandon the security of established strong shapes. Far from being a necessity, syncopation is a daring achievement; it is a delicate balance between prose rhythm and metre. As Fowler asserts: “There can be a situation (Hopkins’s ‘counterpoint’) where the prose rhythm makes itself felt as something playing against the ostensible metre. But extreme lack of fit of words with feet results in the total assertion of prose rhythm” (1966: 94). And, “in Donne, who, according to Chatman, has a much higher pro­portion of reversed feet [than Pope], the tension is less because the metrical pat­tern is obscured” (1966: 93) In trying to achieve ambiguous, complex rhythms, there is always a possibility that the metre will be lost sight of, a risk some poets seem to be unwilling to run.

I submit, then, the following two explanations for Fowler’s generalization about the iambic. First, as we have seen, end-accented metres allow for greater flexibility in manipulating the time-factor in performance than beginning-accented metres. Secondly, bisyllabic feet have “stronger gestalt” than trisyllabic feet; they can more effectively be maintained when conflicting with prose rhythm. When per­forming trisyllabic feet, the reader is inclined to entirely suppress prose rhythm, otherwise the metre of the poem is in danger of disintegration. (This may probably account for the fact that, in “quantitative” measures too, the iambic was found to be most “natural for dialogue”).

Ternary Metres

We have seen that critics are inclined to link the general character of ternary metres with that of the trochaic. We are now in a position to point out the source of their common character. They resemble each other in that they are all unlike the iambic. We have seen that the iambic is “natural for dialogue”, not in that its pat­tern is similar to the stress patterns of ordinary speech, but that it allows the greatest tension between prose rhythm and metre. It has a stronger gestalt than the ternary metres, therefore, the feel of it can be preserved even when the lexical stress pattern strongly deviates from it. In order to preserve the integrity of the larger feet of three syllables, one has to suppress prose rhythm whenever it deviates from a ternary foot.  This is the common factor to ternary metres and the trochaic. We have seen that in the trochaic too, although for different reasons, in order to preserve its peculiar character, one feels inclined to suppress in prose rhythm what­ever deviates from perfect regularity. The greater regularity of ternary metres and the trochaic renders them of a more compelling, though less complex nature.

Finally, I wish to clarify the negative relationship between the iambic and the ternary metres by briefly commenting upon prevailing practice in some languages other than English. Unlike English, where ternary metres are very rare, in modem Hebrew poetry tonic-syllabic amphibrach and anapest are common. The end-­stressed character of the language renders the dactylic so unnatural that it is virtu­ally non-existent (except for translations from classical poetry where, too, it raises almost insurmountable difficulties). The correspondence of stressed syllables with strong positions is usually observed in the anapestic and amphibrachic measures and they are frequently used in highly convergent poems, with the psychological atmosphere of certainty and patent purpose (such as journalistic poetry). In order to prevent monotony and “saturation” in their verse, the poets vary their rhythms by occasionally leaving a weak position unoccupied rather than by displacing a stress from a strong to a weak position; the same poets in the iambic do resort to stress displacement (though less than English poets).

Hungarian poets have free access to both “quantitative” and syllabo-tonic metres. In “quantitative” measures they usually resort to ternary feet, resulting in rather unnatural cadences. Curiously enough, the same poets write iambic verse in syllabo-tonic metre, involving “syncopation” of metric stress and prose rhythm The reason seems to be this. “Quantitative” metre, a relatively recent import to Hungarian, is at variance with the natural rhythms of the Hungarian language. As ternary measures subordinate stress pattern to metre, this means that “quantitative” and ternary measures are alike in that they both demand the suppression of the natural stress pattern of the Hungarian language, and so make, for negative reasons, quite natural bed-fellows.

Another observation on the negative relationship between the iamb and ternary metres concerns the problem of translation from French. The alexandrine, the most widespread metre in French, is syllabic. It consists of twelve syllables (thirteen, in ”feminine”-ended lines), with a compulsory caesura after the sixth. It makes no use of contrast between prominent and non-prominent syllables. French accent falls, typically, on the last syllable of the word, or on the penultimate syllable, if the final syllable is an articulated e mute, or e atone. Alexandrines by Racine, Baudelaire and other French poets are usually translated into iambic hexameter in languages as dissimilar as Hebrew and Hungarian. Once, however, I came across a Hebrew translation of Baudelaire’s “Correspondances” into the amphibrach. The rhythm sounded strikingly unsuitable. It had a vigorous, straightforward quality, quite unlike the vague impression the poem makes in French. One’s first response to such an encounter is surprise. Then it comes to mind: surely it is only a matter of habit that the ear feels the iamb rather than the amphibrach as the tonic-syllabic equivalent of the alexandrine. After all, four times three make twelve just as six times two make twelve. The caesura after the sixth syllable will coincide with a foot boundary, whether binary or ternary.  There appears to be no reason why Baudelaire or Racine should not be translated into the amphibrach. A closer look at the French poem even reveals that the “stress pattern” of the first hemistich confirms the ternary anapest. But the second hemistich confirms the binary iambic. The third one nearly confirms the iambic (except for the “inverted first foot”), while the fourth confirms anapest; and so forth.  Consider the first two lines, indicating the position in which the “stress” occurs:

(14)

In the light of the foregoing discussion, this irregularity becomes meaningful. The alexandrine is similar to the iambic in one important respect. It tolerates greater irregularity of the stress pattern than the trochaic or ternary metres such as the anapest, the dactyl or the amphibrach would tolerate.

To sum up: We have distinguished metric pattern, stress pattern and pattern of performance. When stress pattern and metric pattern converge, they yield strong prosodic gestalts, displaying a psychological quality of certainty and patent purpose. When they diverge, the verse is in danger of falling into chaos. In ternary metres, performers are inclined to subordinate in such cases the prose rhythm to the regular metric beat. The iambic foot, with its stronger gestalt, seems to tolerate greater deviations and complexity. In extreme cases of deviation, the performer needs—in order to prevent chaos—to accommodate the divergent patterns in a strong gestalt of additional grouping. It is some underlying strong gestalt—whether in the pattern of metre, or of performance—that makes rhythmicality possible when divergent elements are present. As psychological experiments have suggested, end-accented metres (as the iambic) allow for greater flexibility in manipulating the time factor than beginning-accented metres (such as the trochaic). Hence the relatively greater rigidity of trochaic verse, manifest in its “compelling” nature observed by so many critics.

References

Anthi Revithiadou  (2004) “The Iambic/Trochaic Law revisited—Lengthening and shortening in trochaic systems”.  In Boban Arsenijevic, Noureddine Elouazizi, Martin Salzmann & Mark de Vos (eds.), Leiden Papers in Linguistics 1.1, 37-62. Available online:

             http://www.let.leidenuniv.nl/pdf/lucl/lwpl/1.1/revithiadou.pdf).

Aristotle, 1932, The Rhetoric of, Lane Cooper, trans. (New York & London: Appleton, Century).

             W. Rhys Roberts trans. Online:

             http://libertyonline.hypermall.com/Aristotle/Rhetoric/Rhetoric.html

Beardsley, Monroe C., 1958. Aesthetics—Problems in the Philosophy of Criticism (New Yolk and Burlingame. Harcourt, Brace & World Inc.).

Beaver, Joseph C. 1968, “A Grammar of Prosody”, College English 29: 310-321.

Chatman, Seymour, 1965 A Theory of Meter (The Hague. Mouton, Janua Linguarum).

Coleridge, Samuel Taylor (1951) Biographia Literaria. In Donald A. Stauffer (ed.) Selected Poetry and Prose. New York: The Modern Library, 109–428.

Fowler, Roger, 1966 “‘Prose Rhythm’ and Metre”, in Roger Fowler ed., Essays  on  Style  and Language (London: RKP).

Fry, D.B., 1958, “Experiments in the Perception of Speech”, Language and Speech 1, 126-151.

             1970 “Speech Reception and Perception”, in John Lyons ed , New Horizons in Linguistics (Harmondsworth: Penguin Books).

Halle, Morris and S. Jay Keyser, 1966, “Chaucer and the Study of Prosody”, College English 28, 187-219.

Hayes, B. (1985). Iambic and trochaic rhythm in stress rules. Niepokuj, N., M. VanClay, V. Nikiforidou, & D. Jeder (eds.), Proceedings of BLS 11: parasession on poetics, metrics, and prosody. BLS, Berkeley, pp.429-446.

Hayes, Bruce (1995). Metrical Stress Theory: Principles and Case Studies. Chicago: The University of Chicago Press.

Herrnstein-Smith, Barbara (1968) Poetic Closure. Chicago: Chicago UP.

Meyer, Leonard B., 1956. Emotion and Meaning in Music (Chicago: Chicago  University).

Rice, C. (1992). Binarity and ternarity in metrical theory: parametric extensions. Doctoral dissertation, University of Texas, Austin, Texas. Available online: http://www.hum.uit.no/a/rice/v2/writing/rice1992.html

Schramm, Wilbur L., 1935.  Approaches to the Science of English Verse (Iowa City: Iowa University).

Tsur, Reuven, 1972  “Articulateness and Requiredness in Iambic Verse”, Style 6, 123-148.

Tsur, Reuven, (1977) A Perception-Oriented Theory of Metre. Tel Aviv: The Porter Institute for Poetics and Semiotics.

Wellek, René and Austin Warren, 1956. “Euphony, Rhythm, and Meter”, in Theory of Literature (New York: Harcourt, Brace).

Woodrow, Herbert (1909). A quantitative study of rhythm. Archives of Psychology (New York) 14, 1-66.

Woodrow, H. 1911 “The Role of Pitch in Rhythm,” Psychological Review , 18 ,54-77 .

Woodrow, H. 1951 ‘‘Time Perception,” in Handbook of Experimental Psychology, S. Stevens (editor), J. Wiley & Sons, New York.

Zhirmunsky, V., 1966. Introduction to Metrics, C. F. Brown, trans. (The Hague: Mouton).